Biological systems are often very complicated and this makes it difficult to establish theories which explain their behaviour. One way to overcome this is to use mathematical modelling. A mathematical model for a biological system is a mathematical construct which mirrors key aspects of the biology while being simpler than the original system, and therefore easier to understand. Once insights about the behaviour of the model have been obtained these can be translated to obtain insights into the biology.
Dynamical systems
In our group we study the time evolution of certain biological systems. The mathematical models which serve this purpose are dynamical systems. They come in different types but what they have in common is that they describe certain quantities depending on a variable representing time. The type of dynamical systems which we have mainly concentrated on up to now are ordinary differential equations. In general they depend on biological parameters such as reaction constants. The aim is to understand the qualitative behaviour of the solutions of the system. Are there steady states and if so how many? When do other solutions converge to steady states? Are all solutions bounded? Are there damped or sustained oscillations?
The choice of models
In models of biochemical systems the unknowns are the concentrations of chemical substances. These take part in various chemical reactions and constitute a reaction network. Making suitable assumptions about the nature of the reactions (kinetics) leads to a system of ordinary differential equations. It often happens that a number of different mathematical models are set up for the same biological system. This leads to the questions of the relations between the different models and criteria for choosing between them. We address these questions in our research. What are the choices which lead to different models? The aim is to obtain a simplification. To do this we discard some substances, considered to be of secondary importance, and retain others. This is necessary since otherwise the number of unknowns and the number of parameters in the model are so great as to make an understanding by purely mathematical techniques or an understanding by computer simulations difficult to obtain. In addition the experimental data available about the values of the parameters is often limited. The information about the reaction mechanisms is also limited and it is necessary to make some choice, such as mass action kinetics.
Maximal simplification (the low throughput approach)
In modern biology high throughput approaches are very popular. This means gathering as much experimental data as possible and then building as much of this data as possible into models. These are in principle mathematical models but in the end computer simulations play the central role. These produce a kind of theoretical data. This situation can be seen as a problem. To quote Nobel laureate Sydney Brenner, 'We are drowning in a sea of data and thirsting for knowledge'. In an alternative approach, which might be called 'low throughput' we try to reduce the system as far as possible while retaining important features. In more detail we can think of a three-step process. In the first step we replace a 'large' model by a 'small' model. In the second step we analyse the small model in as much detail as possible. In the third step we examine to what extent the conclusions obtained for the small model can be extended to the large one. In fact this three-step process comes between the other steps of producing the model starting from the biology and using the mathematical results to suggest biological conclusions.
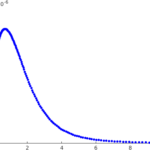
Example 1. T cell activation
T cells are white blood cells which are supposed to distinguish between foreign substances and host substances within an organism and direct the immune system appropriately. How well they accomplish this task has an influence on infectious diseases, autoimmune diseases and cancer. We are studying the initial stage of T cell activation, the first three minutes. A model for this was introduced by Grégoire Altan-Bonnet and Ron Germain. It is a 'big' model, with more than 250 unknowns. Later Paul François and collaborators introduced a much simpler alternative. Together with Eduardo Sontag (at that time at Rutgers University) we studied the model of François et al. mathematically. We were also able to relate the properties of the solutions of this model directly to questions of biological interest. For instance, can it happen that under certain circumstances, a substance which stimulates a T cell more strongly leads to a weaker response? If so can this be based on things which happen during the initial stage and therefore be described by the model of François et al.? We obtained a positive answer to these questions.The model of Altan-Bonnet and Germain is being studied further in the PhD project of Pia Brechmann.
(with E. D. Sontag) Multiple steady states and the form of response functions to antigen in a model for the initiation of T cell activation. R. Soc. open sci. 2017 4 170821. Preprint version.
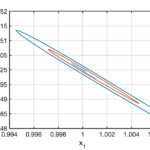
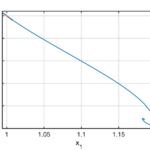
Example 2. Regulation of the activity of the kinase Lck
Immune checkpoint therapy is a promising new approach to fighting cancer in which antibodies are used to strengthen the attack on tumours by T cells.
At present the most successful of these therapies involve the substance PD-1.
Unfortunately the mechanisms by which PD-1 stimulates T cells are poorly understood. Mathematical models may have something to contribute to improving this situation. In an existing mathematical model of this type the substance Lck plays a central role. With this motivation Lisa Kreusser (at that time based at the University of Cambridge, UK) and I set out to study models for the way in which the activity of Lck is controlled. Lck catalyses its own phosphorylation and this can lead to complex dynamics. We proved that a simple model for the activation of Lck exhibits oscillations.
(with L.M. Kreusser) Autophosphorylation and the dynamics of the activation of Lck. Bull. Math. Biol. 83, 64 (2021). Preprint version.

Example 3. The Calvin cycle of photosynthesis
The Calvin cycle is part of photosynthesis. There are many mathematical models of this system and we have investigated their properties and their relations to each other. Recently, in the context of the PhD project of Hussein Obeid, we have studied a case of a maximally simplified model introduced by Brian Hahn. It is two-dimensional and we were able to analyse it in great detail. Bounded solutions always converge to steady states but unbounded solutions can also occur when the process of photorespiration is not included. This gives a mathematical confirmation of the idea of Hahn that photorespiration can stabilize the Calvin cycle. These results have appeared in a journal. In the PhD thesis which arose from this project the results of the published article were extended to other more complicated models of dimension three. It particular it was possible to show that there are no oscillations in this system, which was challenging mathematically. In this work the theory of monotone dynamical systems played a central role.
(with H. Obeid) The minimal model of Hahn for the Calvin cycle. Math. Biosci. Eng. 16, 2353-2370 (2019) Preprint version.
Example 4. A model of the Calvin cycle with diffusion
Some years ago Juan Velazquez and I studied some aspects of the dynamics of two basic models of the Calvin cycle. The following biologically motivated question concerning these models was left open at that time. If this model is modified by adding diffusion of ATP (thus turning the set of ODE into a system of reaction-diffusion equations) does this give rise to new steady states?
Recently Burcu Gürbüz and I wrote a paper in which we gave a positive answer to this question. In fact there can be infinitely many inhomogeneous steady states for given values of the parameters. We also proved that all of these steady states are unstable and thus they cannot play the role envisaged in the original biological motivation.
(with B. Gürbüz) Analysis of a model of the Calvin cycle with diffusion of ATP. Preprint.
(with J. J. L. Velázquez) Dynamical properties of models for the Calvin cycle. J. Dyn. Diff. Eq. 26, 673-705 (2014). Preprint version.
Example 5. Models of hepatitis B and C
With colleagues from Cameroon we have studied models for the dynamics of infectious diseases within a host. With the group of Calvin Tadmon (Dschang) we studied a model for hepatitis B including diffusion of virions and delay effects. It also includes the effect of humoral immunity. We studied the existence and stability of steady states. With the group of Alexis Nangue (Maroua) we studied a model for hepatitis C defined by ordinary differential equations. It includes a simple description of the replication of RNA which is specific to that virus. We studied the existence and stability of steady states and obtained some results on the convergence of more general solutions to steady states. A important mathematical aspect of the arguments is the use of a method of Li and Muldowney.
(with A. Nangue, B. Kammegne Tcheugam, und P. S. Kamdem Simo) Analysis of an initial value problem for an extracellular and intracellular model of hepatitis C virus infection. Preprint.
(with S. Foko und C. Tadmon) Global stability analysis of a delay cell-population model of hepatitis B infection with humoral immune response. Dyn. Sys. 36, 537-559 (2021).
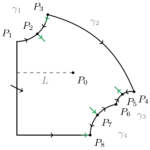
Example 6. The Selkov model of glycolysis
Glycolysis is the process by which living organisms obtain energy from sugar. In some cases a constant input can lead to an oscillatory output. A key step of the process which is the source of the oscillations was modelled by Evgeny Selkov. He wrote down a two-dimensional model with mass action kinetics. This model was studied by Pia Brechmann in her MSc thesis and we published some results of that thesis together with some extensions. They give a rather complete picture of the dynamics of the system. In particular, there exist unbounded solutions for all values of the parameters. One question remained unanswered in this work. Is it the case that, as suggested by Selkov, there are solutions which become unbounded in an oscillatory way, i.e. the trajectory looks like a spiral which expands indefinitely? In a further article we proved that solutions of this type do in fact exist and investigated what happens in the case, also considered by Selkov, where mass action is replaced by Michaelis-Menten kinetics.
(with P. Brechmann) Unbounded solutions of models for glycolysis. J. Math. Biol 82, 1 (2021). Preprint version.
(with P. Brechmann) Dynamics of the Selkov oscillator. Math. Biosci. 306, 152-159 (2018). Preprint version.
Example 7. Phosphorylation systems
In biological systems information is often stored in the phosphorylation states of various proteins. A relatively simple mathematical example of this is the multiple futile cycle where a protein can be phosphorylated at several sites in a way which obeys certain rules. Liming Wang and Eduardo Sontag proved that the number of steady states increases without limit with the number of sites.What was still missing for a long time was a rigorous and sharp lower bound for the number of steady states and a proof of the stability properties of these steady states. With Juliette Hell we proved that in the case of two sites the sharp lower bound for the number of stable steady states is two. Elisenda Feliu, Carsten Wiuf and I recently extended this result to an arbitrary number of phosphorylation states.
(with E. Feliu und C. Wiuf) A proof of unlimited multistability for phosphorylation cycles. Nonlinearity 33, 5629–5658 (2020). Preprint version.
(with J. Hell) A proof of bistability for the dual futile cycle. Nonlin. Analysis: RWA. 24, 175-189 (2015). Preprint version.